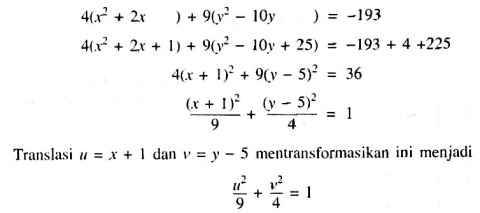TRANSFORMASI SUSUNAN SUMBU
Untuk memindahkan satu titik atau bangun pada bidang dapat dilakukan dengan menggunakan Transformasi. Transformasi Geometri adalah bagian dari geometri yang membicarakan perubahan, baik perubahan letak maupun bentuk penyajianya didasarkan dengan gambar dan matriks. Transformasi Geometri lebih sering disebut transformasi adalah mengubah setiap koordinat titik (titik-titik dari suatu bangun) menjadi koordinat lainnya pada bidang dengan satu aturan tertentu. Misalnya, transformasi T terhadap titik P (x,y) menghasilkan bayangan P’ (x’, y’) operasi tersebut dapat ditulis sebagai :
P (x, y) → P’ (x’, y’)
JENIS-JENIS TRANSFORMASI
Transformasi pada bidang ada 4 macam, yaitu :
1. Translasi ( Pergeseran )
Translasi adalah Transformasi yang memindahkan setiap titik pada bidang menurut jarak dan arah tertentu. Di dalam operasi translasi, bangun geometri bayangan kongruen terhadap bangun geometri semula.
Translasi T dapat dinyatakan dalam bentuk pasangan terurut dua bilangan ab dan dituliskan sebagai:
T = ab
Keterangan:
· a dan b masing-masing disebut sebagai komponen translasi
· a menyatakan komponen translasi dalam arah sumbu X
Ø Jika a > 0, maka arah pergeserannya adalah a satuan ke kanan
Ø Jika a < 0, maka arah pergeserannya adalah |a| satuan ke kiri
· b menyatakan komponen translasi dalam arah sumbu Y
Ø Jika b > 0, maka arah pergeserannya adalah b satuan ke atas
Ø Jika b < 0, maka arah pergeserannya adalah |b| satuan ke bawah
Bayangan titik P (x,y) oleh translasi T = ab adalah P’ (x’ , y’) denganx’= x+a dan y’ = y+b. Bayangan garis y = mx + c oleh translasi T=ab adalah garis y - b = m (x - a) + c.
2. Refleksi ( Pencerminan )
Refleksi adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang akan dipindahkan. Jika sebuah bangun geometri dicerminkan terhadap sebuah garis tertentu, maka bangun bayangan kongruen dengan bangun semula. Pada transformasi refleksi, jarak titik pada bangun bayangan ke sumbu cermin sama dengan jarak titik pada bangun semula ke sumbu cermin.
Cara melukis bayangan dari bangun geometri adalah seagai berikut.
· Tentukan terlebih dahulu sebuah garis yang akan bertindak sebagai sumbu cermin atau sumbu simetri.
· Dari tiap titik sudut geometri yang akan dilukis bayangannya, buatlah garis yang tegak lurus terhadap sumbu cermin.
· Lukislah titik-titik sudut bangun geometri bayangan dengan cara mengukur jarak antara titik sudut bangun geometri bayangan terhadap sumbu cermin sama dengan jarak titik sudut bangun geometri semula terhadap sumbu cermin.
· Hubungkan titik-titik sudut yang berdekatan sehingga diperoleh bangun geometri bayangan.
Persamaan transformasi pada bidang, yaitu
· Persamaaan transformasi terhadap sumbu X
Misalkan titik P(x,y) dicerminkan terhadap sumbu X sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap sumbu X ditentukan oleh hubungan:
x’ = x
y’ = -y
Ditulis : P(x,y) sumbu X P’(x,-y)
· Persamaan transformasi terhadap sumbu Y
Misalkan titik P(x,y) dicerminkan terhadap sumbu Y sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap sumbu Y ditentukan oleh hubungan:
x’ = -x
y’ = y
Ditulis : P(x,y) sumbu Y P’(-x,y)
· Persamaan transformasi refleksi terhadap garis y = x
Misalkan titik P(x,y) dicerminkan terhadap garis y = x sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = x ditentukan oleh hubungan:
x’ = y
y’ = x
Ditulis : P(x,y) y = x P’(y,x)
· Persamaan transformasi refleksi terhadap garis y = -x
Misalkan titik P(x,y) dicerminkan terhadap garis y = -x sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = - x ditentukan oleh hubungan:
x’ = -y
y’ = -x
Ditulis : P(x,y) y = -x P’(-y,-x)
· Persamaan transformasi refleksi terhadap titik asal O(0,0)
Misalkan titik P(x,y) dicerminkan terhadap titik asal O(0,0) sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap titik asal O(0,0) ditentukan oleh hubungan:
x’ = -x
y’ = -y
Ditulis : P(x,y) titik asal O P’(-x,-y)
· Persamaan transformasi refleksi terhadap garis x = h
Misalkan titik P(x,y) dicerminkan terhadap garis x = h sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis x = h ditentukan oleh hubungan:
x’ = 2h -x
y’ = y
Ditulis : P(x,y) x = h P’(2h-x, y)
· Persamaan transformasi refleksi terhadap garis y = k
Misalkan titik P(x,y) dicerminkan terhadap garis y = k sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = k ditentukan oleh hubungan:
x’ = x
y’ = 2k-y
Ditulis : P(x,y) y = k P’(x, 2k-y)
3. Rotasi ( Perputaran )
Rotasi adalah transformasi yang memetakan setiap titik pada bidang ketitik lainnya dengan cara memutar pada pusat titik tertentu. Titik pusat rotasi adalah titik tetap atau titik pusat yang digunakan sebagai acuan untuk menentukan arah dan besar sudut rotasi. Titik pusat dapat berada di dalam, pada, atau di luar bangun geometri yang hendak dirotasi.
Arah rotasi disepakati dengan aturan bahwa jika perputaran berlawanan dengan arah jarum jam, maka rotasi bernilai positif, sedangkan jika perputaran searah jarum jam, maka rotasi bernilai negatif. Besarnya sudut putar rotasi menentukan jauhnya rotasi. Jauh rotasi dinyatakan dalam bilangan pecahan terhadap satu kali putaran penuh (360°) atau besar sudut dalam ukuran derajat atau radian.
Bayangan titik P (x,y) yang dirotasikan terhadap pusat O (0,0) sebesar θ adalah P’(x’ ,y’ ) dengan:
X’ = x cos θ – y sin θ
Y’ = x sin θ + y cos θ
Bayangan titik P (x,y) yang dirotasikan terhadap pusat A (a,b) sebesar θ adalah P’(x’ , y’) dengan:
X’ – a = (x-a) cos θ – (y-b) sin θ
Y’ – a = (x-a) sin θ + (y-b) cos θ
4. Dilatasi ( Perbesaran/ Perkalian)
Ditalasi adalah transformasi yang mengubah ukuran atau skala suatu bangun geometri (pembesaran/pengecilan), tetapi tidak mengubah bentuk bangunan tersebut. Bayangan titik P (x,y) oleh dilatasi [ O, k] adalah P’ (x’ ,y’) dengan X’ = kx dan y’=ky.