PERSAMAAN PARAMETRIK
Kita lanjutkan bahasan kita mengenai Fungsi Paramatrik. Fungsi parametrik adalah fungsi yang dipengaruhi oleh paramater tertentu. misalnya ” t” . Jadi bukan lagi y=f(x) akan tetapi x=f(t) dan y=g(t). Perlunya menggunakan fungsi parametrik adalah karena suatu kurva berubah posisi koordinatnya (x,y) lebih karena dipengaruhi oleh faktor “t”. Sehingga kadang kurva terlihat begitu rumit, model kurva ini dibagi menjadi 4 kelompok.
Berikut ini contoh sebuah fungsi parametrik dan bagaimana membuat gambarnya
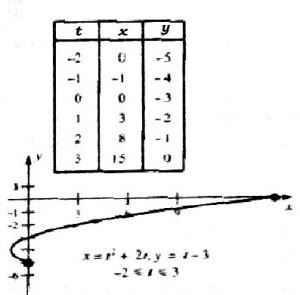
Untuk membuat gambarnya, lebih mudah untuk membuat tabel 3 kolom seperti dibawah ini kemudian baru digambar. Buatlah titik-titik koordinat (x,y) hasil dari memasukkan nilai “t” ke dalam persamaan f(t) dan g(t), kemudian dilanjutkan dengan membentuk kurva yang mulus
Terlihat dari gambar di atas, adalah sebuah kurva parabola. Dan kita bisa mengetahui persamaan parametrik di atas merupakan persamaan parabola atau bukan, dengan mengeliminasi paramater “t”. Caranya sebagai berikut
Contoh lain cara menghilangkan parameter dalam persamaan parametrik
Juga contoh berikut
Aplikasi Turunan dan Integral pada Persamaan Parametrik
Seperti halnya persamaan dalam bentuk y=f(x), maka persamaan parametrik juga bisa diturunkan dan juga diintegralkan. Akan tetapi harus mengikuti beberapa cara berikut
Penurunan Funsi Parametrik
Untuk lebih jelasnya, mari kita perhatikan contoh berikut






Tidak ada komentar:
Posting Komentar