ELLIPS

Menggambar Grafik Elips Horizontal

Sketsalah grafik dari persamaan:

Pembahasan Dengan p ≠ q, persamaan di atas merupakan persamaan elips yang memiliki titik pusat di (2, –1). Jarak horizontal dari titik pusat ke grafik adalah p = 5 dan jarak vertikal dari titik pusat ke grafik adalah q = 3. Setelah memplot titik-titik yang bersangkutan dan menghubungkannya dengan kurva halus, kita dapat mensketsa grafik dari persamaan tersebut sebagai berikut.

Seperti persamaan lingkaran, persamaan elips juga dapat dinyatakan ke dalam bentuk polinomial. Untuk persamaan 25x2 + 4y2 = 100, kita tahu bahwa persamaan ini bukan merupakan persamaan lingkaran karena koefisien-koefisien dari x2 dan y2 tidak sama, dan titik pusat dari grafiknya merupakan titik (0,0) karena a = b = 0. Untuk menggambar grafik dari persamaan seperti itu, kita dapat mengubah persamaan tersebut menjadi bentuk standar.

 Menggambar Grafik Elips Vertikal

Untuk 25x2 + 4y2 = 100, (a) tulislah persamaan tersebut ke dalam bentuk standar dan tentukan titik pusat, nilai p, dan q-nya, (b) identifikasi sumbu mayor dan minornya dan labelilah titik-titik puncaknya, serta (c) gambarkan grafiknya.

Pembahasan Koefisien-koefisien dari x2 dan y2 tidak sama, dan 25, 4, dan 100 memiliki tanda yang sama (positif). Sehingga, persamaan tersebut merupakan persamaan elips dengan pusat di (0, 0). Selanjutnya kita ubah persamaan tersebut ke dalam bentuk standar.

Hasil di atas menunjukkan bahwa p = 2 dan q = 5, yang mengindikasikan bahwa sumbu mayornya vertikal dan sumbu minornya horizontal. Dengan (0, 0) sebagai titik pusat, maka perpotongan grafik terhadap sumbu-x ada di titik-titik (–2, 0) dan (2, 0), sedangkan titik-titik puncaknya (dan perpotongan grafik dengan sumbu-y) ada di titik-titik (0, –5) dan (0, 5). Sehingga grafik dari elips tersebut dapat ditunjukkan oleh gambar berikut.

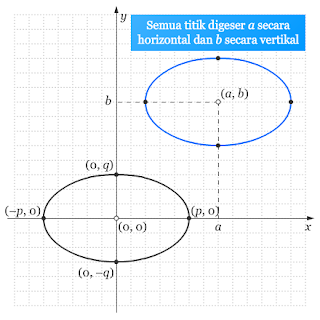
 Jika titik pusat dari elips tidak pada titik asal (0, 0), dalam persamaan bentuk polinomialnya terdapat suku-suku linear sehingga kita harus melengkapkan kuadrat dalam x dan y, kemudian menuliskannya ke dalam bentuk standar untuk menggambar grafiknya. Gambar di bawah ini mengilustrasikan bagaimana elips yang berpusat di titik (0, 0) digeser untuk menjadi elips tertentu.

Semoga bermanfaat :*