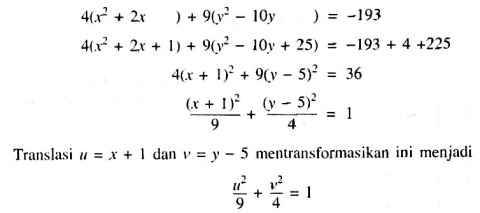KOORDINAT DAN PERSAMAAN KUTUB

PERSAMAAN KUTUB

Contoh persamaan kutub adalah:

r = 8 sinθ 

dan 

r = 2 / ( 1 - cosθ )

Seperti halnya dengan system koordinat siku-siku, kita juga dapat menggambarkan grafik sebuah persamaan kutub. Grafik persamaan kutub adalah himpunan titik-titik yang mempunyai paling sedikit sepasang koordinat kutub yang memenuhi persamaan yang bersangkutan. Salah satu cara untuk menggambar grafik itu adalah dengan menyusun daftar nilai-nilai koordinat, kemudian menggambar titik dengan koordinat-koordinat yang bersangkutan dan akhirnya menghubungkan titik itu dengan sebuah kurva yang mulus.

Contoh 7.1. :
Gambar grafik persamaan kutub r = 8 sin θ
Penyelesaian : Kita ganti kelipatan π/6 untuk θ dan menghitung nilai r yang bersangkutan. Apabila θ naik dari 0 hingga 2π, grafik dilintasi dua kali

Contoh 7.2 

Gambarlah grafik dari 

r = 2 / (1 - cosθ)

Penyelesaian : 

Lihat Gambar dibawah ini Perhatikan gejala yang tidak akan terjadi dengan system koordinat siku-siku. Koordinat (-2, 3π/2) tidak memenuhi persamaan. Walaupun demikian titik P (-2, 3π/2) terletak pada grafik, sebab (2, π/2) merupakan koordinat P dan memang memenuhi persamaan tersebut. Kita dapat menarik kesimpulan bahwa dalam system koordinat kutub, walaupun ada sepasang koordinat tertentu yang tidak memenuhi suatu persamaan, tetapi ini tidak perlu mengakibatkan bahwa titik yang bersangkutan tidak terletak pada grafik persamaan itu. Kenyataan ini mengakibatkan banyak kesulitan; kita harus belajar terbiasa dengan kenyataan tersebut.

Persamaan Kutub untuk Garis, Lingkaran dan Konik

Jika sebuah garis melalui kutub, persamaannya adalah θ = θ₀. Apabila garis tidak melalui kutub, maka garistersebut berjarak misalnya d dari kutub (d>0). Andaikan θ₀ sudut antara sumbu kutub dan garis tegak lurus dari kutub pada garis itu (Gambar 7.9). Apabila P (r, θ) sebuah titik pada garis, maka cos (θ - θ₀) = d/r, atau 

Garis : r = d / ( cosθ - θ₀ ) 

Apabila sebuah lingkaran dengan jari-jari a berpusat di kutub, pesamaannya adalah r = a. Apabila pusatnya di (r₀ , θ₀), persamaannya agak rumit, kecuali kalau kita pilih r₀ = a (Gambar 7.10). Maka menurut hukum kosinus, a² = r² + a² – 2ra cos (θ - θ₀)

yang dapat disederhanakan menjadi : 

Lingkaran : r = 2a cos (θ - θ₀)

Gambar 7.9 (kiri) dan Gambar 7.10 (kanan)

Suatu hal yang menarik jika θ₀ = 0 dan θ₀ = π/2. Yang pertama menghasilkan persamaan r = 2a cos θ ; yang kedua menghasilkan r = 2a cos (θ – π/2) atau r = 2a sin θ. Persamaan terakhir hendaknya dibandingkan dengan Contoh 1. 

Akhirnya kalau sebuah konik (elips, parabol atau hiperbol) diletakkan sedemikian hingga fokusnya berada di kutub, garis arahnya berjarak d satuan dari kutub (Gambar 7.11), maka dengan menggunakan definisi konik, yaitu |PL| =  e |PF| kita akan memperoleh

r = e [d - r cos (θ - θ₀) ]

atau secara setara : Konik : r = ed / ( 1 + e cos (θ - θ₀) )

Gambar 7.11

Ada lagi kasus yang menarik, yaitu untuk θ₀ = 0 dan θ₀ = π/2. Perhatikan bahwa apabila e = 1 dan θ₀ = 0 kita memperoleh persamaan dalam Contoh 7.2. Hasil di atas kita ikhtisarkan dalam diagram berikut: 

Grafik Persamaan Kutub  

Grafik persamaan kutub yang telah dibahas sebelumnya terdiri atas garis, lingkaran dan konik. Sekarang kita akan membahas grafik-grafik yang lebih rumit bentuknya, yaitu kardioid, limason, mawar dan spiral. Walaupun bentuk grafiknya rumit, namun persamaannya tetap sederhana kalu digunakan persamaan kutub. Dituangkan dengan koordinat siku-siku, persamaannya tidak lagi sederhana. Jadi kita dapat melihat keuntungan adanya system koordinat ini. Ada kurva-kurva yang persamaannya sederhana dalam suatu system dan ada kurva yang persamaannya sederhana dalam system lain. Sifat demikian akan kita gunakan kelak untuk memecahkan suatu persoalan dengan memilih suatu system koordinat yang tepat.

Sifat simetri dapat membantu kita menggambar sebuah grafik. Di bawah ini ada beberapa pengujian kesimetrian yang cukup dalam koordinat kutub. Kebenarannya dapat dilihat pada gambar yang bersangkutan. 

1. Grafik persamaan kutub simetri terhadap sumbu x (yaitu sumbu kutub dan perpanjangannya ke kiri) apabila θ diganti dengan –θ menghasilkan persamaan yang sama (Gambar 7.13). 

2. Grafik persamaan kutub simetri terhadap sumbu y (yaitu garis θ = π/2) apabila θ diganti dengan π-θ menghasilkan persamaan yang sama (Gambar 7.14). 

3. Grafik persamaan kutub simetri terhadap titik asal, apabila r diganti –r menghasilkan persamaan yang sama (Gambar 7.15). 

Karena penggambaran banyak titik di dalam koordinat kutub, maka kemungkinan adanya simetri tidak teridentifikasi oleh ketiga tes ini.

Gambar 7.14 ( kiri ) , Gambar 7.15 ( tengah ) , Gambar 7.15 ( kanan ) 

KOORDINAT DAN PERSAMAAN KUTUB

KOORDINAT KUTUB

Sistem Koordinat Kutub

Dua orang Perancis yaitu Pierre Fermat dan Rene Descartes, telah memperkenalkan system koordinat yang sekarang kita kenal dengan sebutan system koordinat Cartesius atau siku-siku. Dasar pemikiran mereka ialah untuk menunjukkan kedudukan titik P pada bidang dengan dua bilangan yang ditulis dengan lambang (x,y) setiap bilangan menggambarkan jarak berarah dari dua sumbu yang tegak lurus sesamanya (Gambar 7.1). Sistem koordinat ini adalah dasar dari geometri analitik, dan sangat membantu pengembangan kalkulus diferensial dan kalkulus integral yang kita capai hingga saat ini.

Dengan memberikan jarak berarah dari dua sumbu yang tegak lurus bukanlah satusatumya jalan untuk menunjukkan kedudukan suatu titik pada bidang. Cara lain adalah menggunakan apa yang disebut koordinat kutub.

gambar 7.1                                                                                     gambar 7.2

Koordinat Kutub

              Kita mulai dengan menggambar sebuah setengah-garis tetap yang dinamakan sumbu kutub yang berpangkal pada sebuah titik 0. Titik ini disebut kutub atau titik asal. Biasanya sumbu kutub ini kita gambar mendatar dan mengarah ke kanan dan oleh sebab itu sumbu ini dapat disamakan dengan sumbu x positif pada sebuah system koordinat siku-siku. Setiap titik P (selain dari kutub) adalah perpotongan antara sebuah lingkaran tunggal yang berpusat di 0 dan sebuah sinar tunggal yang memancar dari 0. Jika r adalah jari-jari lingkaran dan θ adalah salah satu sudut antara sinar dan sumbu kutub, maka (r, θ) dinamakan sepasang koordinat kutub dari titik P (Gambar 7.2).  

       Titik-titik yang dilukiskan oleh koordinat kutub paling mudah digambar apabila kita menggunakan kertas grafik kutub. Pada kertas demikian telah tergambar lingkaranlingkaran yang sepusat dan sinar-sinar yang memancar dari pusat itu. Kita dapat melihatnya pada Gambar 4.3, pada gambar ini telah terlukis beberapa titik.

Gambar 7.3 (kiri) dan Gambar 7.4 (kanan)

Perhatikan sebuah sifat berikut yang tidak ada pada sebuah system koordinat Cartesius. Tiap titik memiliki banyak koordinat kutub. Ini adalah akibat sifat bahwa sudut-sudut θ + 2πn, n = 0, ±1, ±2,…memiliki kaki-kaki yang sama. Misalnya, titik dengan koordinat kutub (4, π/2) juga memiliki koordinat (4, 5π/2), (4, 9π/2), (-4,3π/2), dan seterusnya. Bahkan hal ini berlaku juga jika r diperbolehkan memiliki nilai yang negatif. Dalam hal ini (r, θ) terletak pada sinar yang berlawanan arah dengan  sinar yang dibentuk oleh θ dan yang terletak r satuan dari titik asal. Dengan demikian, titik dengan koordinat kutub (-3, π/6) dapat kita lihat pada Gambar 4.4,  sedangkan (-4, 3π/2) adalah koordinat lain untuk (4, π/2). Titik asal mempunyai koordinat (0, θ), di mana θ sudut sembarang.

Hubungan dengan Koordinat Cartesius

Andaikan sumbu kutub berimpit dengan sumbu x positif system koordinat Cartesius. Maka koordinat kutub (r, θ) sebuah titik P dan koordinat Cartesius (x, y) titik itu dihubungkan oleh persamaan :

x = r cos θ

r² = x² + y²

 y = r sin θ

tan θ = x/y

Hubungan tersebut jelas berlaku untuk sebuah titik P yang berada di dalam kuadran pertama, yang dapat kita lihat pada Gambar 4.7. mudah dibuktikan untuk titik-titik dalam kuadran lain.

Gambar 7.7 (kiri) dan Gambar 7.8 (kanan)

Contoh 7.3 

Tentukan koordinat Cartesius dari titik yang koordinat kutubnya adalah (4, π/6). Tentukan juga koordinat kutub titik yang koordinat Cartesiusnya adalah (-3, 3 ). 

Penyelesaian : 

Jika (r, θ) = (4, π/6), maka 

x = 4 cos π/6 = 4 . √3 / 2= 2 √3 

y = 4 sin π/6 = 4 . ½ = 2 

Jika, (x, y) = (-3, 3 ) , maka 

r² = (-3)2 + ( √3 )2 = 12 

tan θ = √3 / -3 

Salah satu nilai (r, θ) adalah (2√3 , 5π/6). Nilai lainnya adalah (-2√3 , -π/6). 

Ada kalanya grafik persamaan kutub dapat kita lukis dengan mencari persamaannya dalam system Cartesius. Sebagai contoh kita sajikan kasus di bawah ini.

Contoh 7.4 

Buktikan bahwa grafik persamaan r = 8 sin θ (Contoh 1) adalah sebuah lingkaran dan bahwa grafik persamaan r = 2 / (1- cos θ) (Contoh 2) adalah sebuah parabol dengan jalan menulis persamaan Cartesius kurva tersebut. 

Penyelesaian : 

Kalikan ruas kiri dan kanan persamaan r = 8 sin θ dengan r, kita peroleh 

r² = 8r sin θ

dalam bentuk Cartesius persamaan tersebut, menjadi : 

x² + y² = 8y

dan persamaan ini dapat diubah sebagai berikut : 

x² + y² - 8y = 0

x² + y² - 8y  + 16 = 16

x² + (y - 4)² = 16

Persamaan terakhir ini adalah persamaan lingkaran yang berpusat di (0, 4) dan berjari-jari 4. 

PERHATIKAN 

Karena r bisa bernilai 0, ada kesalahan yang mungkin terjadi dalam mengalikan kedua sisi pada suatu persamaan kutub dengan r atau dalam membagi kedua bagian tersebut dengan r. Pada kasus yang pertama, kita dapat menambahkan kutub pada grafik; pada kasus kedua, kita dapat menghilangkan kutub dari grafik. Dalam Contoh di atas, kita kalikan kedua sisi dari r = 8 sin θ dengan r tanpa menimbulkan kesalahan karena kutubnya telah terdapat pada grafik sebagaimana titik dengan koordinat-θ 0. 

Persamaan kedua kita ubah berturut-turut sebagai berikut : 

r = 2 / (1 - cosθ) 

r – r cos θ = 2 

r - x = 2 

r = x + 2

r² = x² + 4x + 4

x² + y² = x² + 4x + 4

y² = 4(x + 1)

Kita lihat bahwa persamaan terakhir ini adalah persamaan parabol dengan puncak di (-1, 0) dan dengan fokus di (0, 0).

Setelah ini kita akan membahas bagimana persamaan kutub. soo ditunggu ya :) karna aku postingnya subuh. yukkk sholat dulu :)

ROTASI SUMBU

Definisi ROTASI

         Rotasi adalah perputaran benda pada suatu sumbu yang tetap, misalnya perputaran gasing dan perputaran bumi pada poros/sumbunya. Untuk bumi, rotasi ini terjadi pada garis/poros/sumbu utara-selatan (garis tegak dan sedikit miring ke kanan). Jadi garis utara-selatan bumi tidak berimpit dengan sumbu rotasi bumi, seperti yang terlihat pada "globe bola dunia" yang digunakan dalam pelajaran ilmu bumi/geografi. Kecepatan putaran ini diukur oleh banyaknya putaran per satuan waktu. Misalnya bumi kita berputar 1 putaran per 24 jam. Untuk rotasi mesin yang berputar lebih cepat dari rotasi bumi, kita pakai satuan rotasi per menit (rpm).

         Akibat dari gerak rotasi ini, maka benda tersebut akan mengalami gaya sentrifugal, yaitu jenis gaya dalam ilmu fisika yang mengakibatkan benda akan terlempar keluar. Hal ini akan nampak terasa pada saat kita naik mobil yang melewati tikungan melingkar. Pada saat mobil ini bergerak melingkar dengan kecepatan agak tinggi, maka penumpang dalam mobil akan merasa terlempar ke samping (ke sisi luar lingkaran itu) sebagai akibat dari adanya gaya sentrifugal.

ROTASI SUMBU

Terlihat bahwa koordinat-uv merupakan koordinat-xy yang diputar ke kiri sejauh (ø + θ) derajad. Lalu bagaimana transformasi koordinatnya ?

Contoh 3 :

Carilah persamaan dalam koordinat-uv dari persamaan xy=1, setelah sumbu diputar sebesar θ = π/4 atau 45 derajad

Solusi :

Gunakan rumus di atas

Dan gambarnya menjadi

Bagaimana jika yang diberikan adalah hanya sebuah persamaan seperti ini (persamaan umum konik)

Jika menggunakan translasi tidak mungkin karena ada komponen campuran (kotak merah), jadi harus dirotasi. Jika dirotasi berapa sudutnya ? Karena tidak ada informasi tentang sudut, hanya persamaan itu saja.

Langkah-langkah menetuka sudut rotasi

Kemudian x dan y dalam fungsi uv diamsukkan ke dalam persamaan diatasnya. Kemudian persamaan disederhanakan menjadi

Dan masih ada komponen campuran yaitu b(uv). Agar nilai ini “0” maka b=0, sedangkan nilai be dihasilkan dari

Agar

Jika b sudah sama dengan 0, maka persamaan bisa diselesaikan dengan/tanpa translasi

Contoh 4 :

solusi

Sketsa gambarnya adalah :

Sekian untuk BAB IV. Terimakasih atas kunjungan kalian. semoga bermanfaat ya :)

nanti kita teruskan lagi

see you soon :*

TRANSLASI SUMBU

TRANSLASI ( PERGESERAN )

      Menggeser atau mentranslasikan suatu gambar sudah dikenal pada pelajaran matematika sebelumnya, pada saat mempelajari pergeseran pusat lingkaran

Jadi penggambaran lingkaran (x-2)²+(y-3)²=25, pada koordinat-xy akan sama dengan u²+v²=25, pada koordinat-uv, yang mana sumbu-u sama dengan garis y=3 sedangkan sumbu-x sama dengan garis x=2.

Jadi jika sumbu baru (uv) dipilih sebagai translasi dari sumbu originalnya (xy), maka setiap titik akan memiliki dua macam koordinat. Satu dalam sumbu lama dan yang lainnya dalam sumbu yang baru

Pada gambar di atas terlihat bahwa titik P dapat dinotasikan dalam dua macam koordinat, yaitu dalam xy dan uv. Yang mana hubungan antara uv dan xy adalah

u=x-h  dan  v=y-k , atau

x=u+h dan y=v+k

Contoh 1 :

Buatlah translasi untuk menghilangkan suku2 berderajad 1

Solusinya

Gambarnya seperti ini

Contoh 2 :

Gunakan translasi untuk menyederhanakan persamaan berikut :

y² – 4x – 12y + 28 = 0

Kemudian tentukan bentuk konik nya, dan sketsa grafiknya !

Solusinya

Translasinya u=x+2 dan v=y-6, sehingga persamaannya menjadi
v² = 4u
Yaitu sebuah parabola horizonral, terbuka ke kanan dengan p=1. Dan inilah sketsa gambarnya

Setelah ini kita akan membahas Rotasi Sumbu. jadi ditunggu ya :)

TRANSFORMASI SUSUNAN SUMBU

TRANSFORMASI SUSUNAN SUMBU

       Untuk memindahkan satu titik atau bangun pada bidang dapat dilakukan dengan menggunakan Transformasi. Transformasi Geometri adalah bagian dari geometri yang membicarakan perubahan, baik perubahan letak maupun bentuk penyajianya didasarkan dengan gambar dan matriks. Transformasi Geometri lebih sering disebut transformasi adalah mengubah setiap koordinat titik (titik-titik dari suatu bangun) menjadi koordinat lainnya pada bidang dengan satu aturan tertentu. Misalnya, transformasi T terhadap titik P (x,y) menghasilkan bayangan P’ (x’, y’) operasi tersebut dapat ditulis sebagai :

P (x, y) → P’ (x’, y’)

JENIS-JENIS TRANSFORMASI

Transformasi pada bidang ada 4 macam, yaitu :

1. Translasi ( Pergeseran )

      Translasi adalah Transformasi yang memindahkan setiap titik pada bidang menurut jarak dan arah tertentu. Di dalam operasi translasi, bangun geometri bayangan kongruen terhadap bangun geometri semula.

Translasi T dapat dinyatakan dalam bentuk pasangan terurut dua bilangan ab dan dituliskan sebagai:

T = ab

Keterangan:

·         a dan b masing-masing disebut sebagai komponen translasi

·         a menyatakan komponen translasi dalam arah sumbu X

Ø  Jika a > 0, maka arah pergeserannya adalah a satuan ke kanan

Ø  Jika a < 0, maka arah pergeserannya adalah |a| satuan ke kiri

·         b menyatakan komponen translasi dalam arah sumbu Y

Ø  Jika b > 0, maka arah pergeserannya adalah b satuan ke atas

Ø  Jika b < 0, maka arah pergeserannya adalah |b| satuan ke bawah

Bayangan titik P (x,y) oleh translasi T = ab adalah P’ (x’ , y’) denganx’= x+a dan y’ = y+b. Bayangan garis y = mx + c oleh translasi T=ab adalah garis y - b = m (x - a) + c.

2. Refleksi ( Pencerminan )

       Refleksi adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang akan dipindahkan. Jika sebuah bangun geometri dicerminkan terhadap sebuah garis tertentu, maka bangun bayangan kongruen dengan bangun semula. Pada transformasi refleksi, jarak titik pada bangun bayangan ke sumbu cermin sama dengan jarak titik pada bangun semula ke sumbu cermin.

Cara melukis bayangan dari bangun geometri adalah seagai berikut.

· Tentukan terlebih dahulu sebuah garis yang akan bertindak sebagai sumbu cermin atau sumbu simetri.

· Dari tiap titik sudut geometri yang akan dilukis bayangannya, buatlah garis yang tegak lurus terhadap sumbu cermin.

· Lukislah titik-titik sudut bangun geometri bayangan dengan cara mengukur jarak antara titik sudut bangun geometri bayangan terhadap sumbu cermin sama dengan jarak titik sudut bangun geometri semula terhadap sumbu cermin.

· Hubungkan titik-titik sudut yang berdekatan sehingga diperoleh bangun geometri bayangan.

Persamaan transformasi pada bidang, yaitu

· Persamaaan transformasi terhadap sumbu X

Misalkan titik P(x,y) dicerminkan terhadap sumbu X sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap sumbu X ditentukan oleh hubungan:

x’ = x

y’ = -y

Ditulis : P(x,y) sumbu X  P’(x,-y)

·         Persamaan transformasi terhadap sumbu Y

Misalkan titik P(x,y) dicerminkan terhadap sumbu Y sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap sumbu Y  ditentukan oleh hubungan:

x’ = -x

y’ = y

Ditulis : P(x,y) sumbu Y  P’(-x,y)

·         Persamaan transformasi refleksi terhadap garis y = x

Misalkan titik P(x,y) dicerminkan terhadap garis y = x  sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = x  ditentukan oleh hubungan:

x’ = y

y’ = x

Ditulis : P(x,y) y = x  P’(y,x)

·         Persamaan transformasi refleksi terhadap garis y = -x

Misalkan titik P(x,y) dicerminkan terhadap garis y = -x  sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = - x  ditentukan oleh hubungan:

x’ = -y

y’ = -x

Ditulis : P(x,y) y = -x  P’(-y,-x)

·         Persamaan transformasi refleksi terhadap titik asal O(0,0)

Misalkan titik P(x,y) dicerminkan terhadap titik asal O(0,0) sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap titik asal O(0,0)  ditentukan oleh hubungan:

x’ = -x

y’ = -y

Ditulis : P(x,y) titik asal O  P’(-x,-y)

·         Persamaan transformasi refleksi terhadap garis x = h

Misalkan titik P(x,y) dicerminkan terhadap garis x = h  sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis x = h  ditentukan oleh hubungan:

x’ = 2h -x

y’ = y

Ditulis : P(x,y) x = h  P’(2h-x, y)

·         Persamaan transformasi refleksi terhadap garis y = k

Misalkan titik P(x,y) dicerminkan terhadap garis y = k sehingga diperoleh bayangan titik P’(x’,y’). Persamaan transformasi terhadap garis y = k ditentukan oleh hubungan:

x’ = x

y’ = 2k-y

Ditulis : P(x,y) y = k  P’(x, 2k-y)

3. Rotasi ( Perputaran )

       Rotasi adalah transformasi yang memetakan setiap titik pada bidang ketitik lainnya dengan cara memutar pada pusat titik tertentu. Titik pusat rotasi adalah titik tetap atau titik pusat yang digunakan sebagai acuan untuk menentukan arah dan besar sudut rotasi. Titik pusat dapat berada di dalam, pada, atau di luar bangun geometri yang hendak dirotasi.

Arah rotasi disepakati dengan aturan bahwa jika perputaran berlawanan dengan arah jarum jam, maka rotasi bernilai positif, sedangkan jika perputaran searah jarum jam, maka rotasi bernilai negatif. Besarnya sudut putar rotasi menentukan jauhnya rotasi. Jauh rotasi dinyatakan dalam bilangan pecahan terhadap satu kali putaran penuh (360°) atau besar sudut dalam ukuran derajat atau radian.

Bayangan titik P (x,y) yang dirotasikan terhadap pusat O (0,0) sebesar θ adalah P’(x’ ,y’ ) dengan:

X’ = x cos θ – y sin θ

Y’ = x sin θ + y cos θ

Bayangan titik P (x,y) yang dirotasikan terhadap pusat A (a,b) sebesar θ adalah P’(x’ , y’) dengan:

X’ – a = (x-a) cos θ – (y-b) sin θ

Y’ – a = (x-a) sin θ + (y-b) cos θ

4. Dilatasi ( Perbesaran/ Perkalian)

         Ditalasi adalah transformasi yang mengubah ukuran atau skala suatu bangun geometri (pembesaran/pengecilan), tetapi tidak mengubah bentuk bangunan tersebut. Bayangan titik P (x,y) oleh dilatasi [ O, k] adalah P’ (x’ ,y’) dengan X’ = kx dan y’=ky.

PARABOLA

Definisi Parabola

Parabola adalah tempat kedudukan titik (himpunan titik) yang berjarak sama

terhadap suatu titik dan suatu garis tertentu. Titik tertentu itu disebut Fokus (F), dan garis

tetap itu disebut Direktrik

Berdasarkan defenisi di atas, kita dapat melukis parabola titik demi titik dengan langkah-langkah

sebagai berikut :  

1. Tetapkan garis g dan titik F .

2. Tarik sebuah garis melalui titik F (diperoleh sumbu x) tegak lurus (┴) garis g sehingga garis 

ini memotong g di s.

3. Titik O (0,0) pada garis FS, sehingga |OS| = |OF|

4. Buatlah lingkaran yang berpusat di F dan berjari-jari r > OF   

5. Lakukan seperti langkah 4*) dari titik S sehingga memotong SF di A₁.

6. Buatlah garis tegak lurus SF sehingga memotong busur lingkaran A pada titik B_1, B₁ adalah salah satu pada parabola . 

7. Ulangi langkah no. 4, 5, dan 6 untuk mendapatkan titik lain pada parabola.

8. Setelah beberapa titik ditemukan, hubungkanlah titik itu dengan sebuah kurva yang mulus, 

kurva itulah disebut parabola .

PERSAMAAN PARABOLA

- Garis g disebut direktrik 

- Titik F(p,0) disebut fokus 

- Titik O(0,0) disebut puncak

- FS disebut sumbu simetri 

- FS = 2p = Parameter

- AB garis yang disebut latus rectum, tegak lurus sumbu parabola melalui titik F. Panjang latus rectum = |4p|.

Dari keterangan gambar diatas, dapat diturunkan persamaan parabola sebagai berikut :  

Parabola  y² = 4px

x²= 4py

HIPERBOLA

Persamaan Garis Singgung Hiperbola

Persamaan Garis Singgung Hiperbola Sebuah garis digambarkan pada sebuah hiperbola. Salah satu kedudukan yang mungkin antara garis itu dan hiperbola adalah garis menyinggung hiperbola. Coba perhatikan gambar berikut.

Pada gambar tersebut garis g menyinggung hiperbola pada titik R(x1, y1).

Persamaan garis singgung yang melalui suatu titik pada hiperbola

• Persamaan garis singgung pada suatu titik R(x1, y1) pada hiperbola

x2a2 − y2b2 = 1

adalah

x1xa2 − y1yb2 = 1

agar kamu lebih paham, coba lihat contoh berikut :

Coba tentukan persamaan garis singgung pada titik (9, 2) yang terletak pada hiperbola

 

(y + 2)248 − (x − 5)212 = 1

Penyelesaian:
Persamaan garis singgungnya dapat dihitung seperti berikut.

(y 1− q)(y − q)a2 − (x1 − p)(x − p)b2= 1(2+ 2)(y + 2)48 − (9 − 5)(x − 5)12= 1(y + 2)12 − (x − 5)3= 1

y – 4x + 10 = 0
Jadi, persamaan garis singgungnya adalah y – 4x + 10 = 0.

Persamaan garis singgung bergradien m pada hiperbola

Misalkan garis g yang menyinggung hiperbola tersebut bergradien m, maka:

x2100−y264=1

Agar kamu lebih paham, coba cermati contoh soal berikut.

Tentukan persamaan garis singgung dengan gradien 1 pada hiperbola

 

x2100−y264=1

Penyelesaian:

Gradien m = 1

Persamaan garis singgungnya adalah sebagai berikut.

y=mx±a2m2−b2−−−−−−−−√y=x±100.1−64−−−−−−−−−√y=x±36−−√y=x±6

Jadi, persamaan garis singgungnya adalah y = x + 6 atau y = x – 6.

demikianlah pembahasan kita mengenai HIPERBOLA.

Semoga bermanfaat ya :)

tunggu postingan yang lainnya jugaa :)