Kedudukan Titik-titik dan Jarak antara Dua Titik

Menyelesaikan Masalah Mengenai Kedudukan Titik-titik dan Jarak antara Dua Titik dengan menggunakan Polya

Hai.. Kali ini kita akan membahas bagaimana Menyelesaikan Masalah Mengenai Kedudukan Titik-titik dan Jarak antara Dua Titik dengan menggunakan Polya. Sebelum itu kita harus memahami bagaimana menyelesaikan masalah dengan polya. 

Pemecahan Masalah Polya

Pemecahan masalah (problem solving) merupakan suatu prosedur untuk menemukan penyelesaian yang tepat atas suatu masalah. Prosedur tersebut pertama kali diformulasikan oleh George Polya (1887 - 1985) seorang guru dan ahli matematika yang menyatakan bahwa ada empat tahap pemecahan masalah yaitu :  understand the problem, devise a plan, carry out the plan, dan look back sebagai berikut :

1)        Understanding the Problem

Tahap pertama yang dilakukan untuk memecahkan masalah adalah memahami masalah. Cara yang disarankan Polya untuk memahami masalah dengan baik yaitu dengan menjawab pertanyaan-pertanyaan berikut :

a.         Nyatakan masalah dengan kalimatmu sendiri !

b.        Tentukan apa saja yang akan ditemukan/dicari/diselesaikan !

c.         Apa saja yang tidak diketahui dari permasalahan itu ?

d.        Informasi apa saja yang kamu peroleh dari permasalahan itu ?

e.         Informasi apa saja yang tidak ada / hilang dari permasalahan itu ?

f.         Informasi apa saja yang tidak dibutuhkan dari permasalahan itu ?

2)        Devising a Plan

Tahap kedua pemecahan masalah adalah menentukan rencana penyelesaian berupa strategi-strategi pemecahan masalah. Beberapa strategi pemecahan masalah antara lain :

a.         Menemukan pola

b.        Menguji masalah yang relevan dan memeriksa apakah teknik yang sama dapat digunakan untuk menyelesaikan permasalahan

c.         Menguji masalah yang lebih sederhana atau khusus dari permasalahan itu dan diperbandingkan dengan penyelesaian masalah sebenarnya

d.        Membuat tabel

e.         Membuat diagram / gambar

f.         Menebak dan memeriksa (guess and check / trial and error)

g.        Menggunakan persamaan (equation) matematika

h.        Bekerja mundur (work backward)

i.          Mengidentifikasi bagian dari hasil (subgoal)

3)        Carrying Out the Plan

Tahap ketiga pemecahan masalah terdiri dari tiga aktivitas yaitu :

a.         Menerapkan satu atau lebih strategi pemecahan masalah untuk menemukan penyelesaian atau perhitungan

b.        Memeriksa setiap langkah strategi yang digunakan baik secara intuitif maupun dengan bukti formal

c.         Menjaga keakuratan proses pemecahan masalah

4)        Looking Back

Langkah terakhir pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya dengan cara :

a.         Memeriksa dengan pembuktian

b.        Menginterpretasikan penyelesaian/solusi berdasarkan permasalahan berdasarkan rasional atau pun argumentasi (reasonable)

c.         Jika memungkinkan lakukan pengujian untuk masalah lain yang relevan atau pun yang lebih umum dengan menggunakan teknik/strategi pemecahan masalah tersebut

Kedudukan Titik-titik dan Jarak antara Dua Titik

Gambar 7. Representasi Titik yang Berpindah posisi Konsep titik diperkenalkan dalam geometri Euclid sebagai elemen yang tidak didefinisikan dan tidak memiliki dimensi panjang. Euclid mendefinisikan titik dalam buku I - Element yaitu “a point is that which has no part”.

Geometri Euclid hanya membahas sifat titik yang diam/tetap, sedangkan geometri analitik juga menelaah sifat-sifat titik yang bergerak seperti yang terjadi di alam. Misalnya sebuah bola yang menggelinding pada permukaan bidang miring dapat dinyatakan sebagai sebuah titik yang bergerak sehingga titik tersebut mengalami perpindahan tempat. Posisi bola saat di bagian atas tidak sama dengan posisi bola saat berada di pertengahan bidang. Proses menelaah sifat titik-titik di berbagai posisi tersebut maka dibutuhkan bantuan aljabar untuk menyatakan posisi titik dalam suatu simbol tertentu.

Gambar 8. Representasi Koordinat Peta

Gambar 8. Representasi Koordinat Peta

Metode yang digunakan untuk menunjukkan posisi sebuah titik pada sebuah bidang mirip seperti teknik menggambar peta. Posisi suatu tempat pada permukaan bumi dinyatakan oleh koordinat peta yaitu derajat lintang (arah utara atau selatan) dan derajat bujur (arah timur atau barat). Posisi acuan untuk koordinat bujur-lintang tersebut yaitu Kota Greenwich di Inggris. Perhatikan gambar dan penjelasan di bawah ini. Misalkan kurva NGAS adalah meridian utama, kurva AWBE adalah garis ekuator, dan titik G adalah kota Greenwich maka posisi kota P dapat dinyatakan sebagai koordinat peta apabila derajat AB dan BP diketahui. Andaikan AB = 70° dan BP = 45° maka posisi P dinyatakan sebagai 70° bujur timur dan 45° lintang utara.

Geometri analitik menyederhanakan koordinat peta tersebut dengan menggunakan dua garis lurus berpotongan untuk menggantikan kurva meridian dan kurva ekuator. Titik potong kedua garis dijadikan sebagai titik acuan biasanya dinyatakan sebagai titik O. Posisi titik P dinyatakan oleh panjang ruas garis BP yang sejajar dengan garis sumbu X¢X dan panjang ruas garis AP yang sejajar garis sumbuYY¢. Panjang ruas garis BP sama dengan panjang ruas garis

Gambar 9. Representasi Titik dalam Sistem Koordinat

OA. Panjang ruas garis AP sama dengan panjang ruas garis OB. Sehingga titik P dapat dinyatakan berada pada posisi sejauh panjang OA dan OB terhadap titik O. 

Dua buah titik berbeda akan berada pada posisi yang berbeda. Jarak kedua titik tersebut dapat ditentukan dengan langkah-langkah sebagai berikut :

•  Buatlah dua titik berbeda yaitu A dan B lalu hubungkan dengan sebuah ruas garis.
• Buat sebuah garis melalui A dan sebuah garis lain yang melalui B sehingga kedua garis berpotongan tegak lurus.
• Tentukan titik potong kedua garis yaitu C sehingga diperoleh segitiga siku-siku ACB atau BCA lalu ukur panjang ruas garis CA dan CB
• Tentukan panjang ruas garis AB dengan menggunakan Teorema Phytagoras 

Titik-titik pada sebuah bidang yang membentuk himpunan titik dan memenuhi suatu kriteria tertentu dinamakan kedudukan titik (locus of points). Kedudukan titik dapat dinyatakan sebagai suatu fungsi. Misalnya titik-titik pada lingkaran berjari-jari 1 cm dapat dinyatakan sebagai x² + y² = 1. Secara geometris, hanya titik-titik berjarak 1 cm dari titik pusat lingkaran tersebut yang memenuhi kedudukan titik yang dinyatakan oleh persamaan x² + y² = 1. Teorema-teorema dasar tentang kedudukan titik-titik (Fundamental Locus Theorems) sebagai berikut.

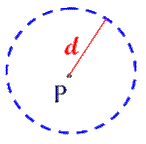
Teorema 1.1 Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah titik P adalah sebuah lingkaran berpusat di titik P dengan ukuran panjang jari-jari d
Teorema 1.2 Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah garis l  adalah sepasang garis-garis sejajar yang masing-masing berjarak d dari garis l
Teorema 1.3 Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garis  dan membagi  menjadi dua bagian sama besar
Teorema 1.4 Kedudukan titik-titik yang berjarak sama dari dua garis yang sejajar yaitu l1 dan l2 merupakan sebuah garis diantara keduanya dan sejajar dengan kedua garis tersebut.
Teorema 1.5 Kedudukan titik-titik yang berjarak sama terhadap dua garis yang berpotongan yaitu l1 dan l2, adalaha sepasang ruas garis (disebut bisectors) yang membagi dua sama besar sudut-sudut yang yang dibentuk garis l1 dan l2
Teorema 1.6 Kedudukan titik-titik yang berjarak sama dari kedua sisi sebuah sudut adalah sebuah ruas garis yang membagi dua sudut tersebut (bisector of angle)
Teorema 1.7 Kedudukan titik-titik yang berjarak sama dari dua buah lingkaran konsentris (concentric circles) adalah sebuah lingkaran yang konsentris terhadap kedua lingkaran tersebut dan berada tepat di tengah keduanya
Teorema 1.8 Kedudukan titik-titik pada jarak tertentu dari sebuah lingkaran yang memiliki jari-jari lebih panjang dari jarak tersebut merupakan sebuah pasangan lingkaran konsentris, di mana masing-masing kedudukan titik tersebut berada di salah satu sisi lingkaran pada jarak tertentu tersebut.
Teorema 1.9 Kedudukan titik-titik yang berjarak tertentu dari suatu lingkaran berjari-jari kurang dari jarak tersebut merupakan sebuah lingkaran yang berada di luar lingkaran pertama dan saling konsentris.

Pembuktian Teorema 1.3

Tahap 1        :  Akan dibuktikan untuk sembarang titik pada kedudukan tersebut memenuhi kondisi-kondisi berikut :

Diketahui    :  Titik A dan B

                       Ruas garis CD   tegak lurus dan membagi ruas garis AB

Ditanyakan :  Apakah untuk sembarang titik P pada ruas garis CD berjarak sama dari A dan B yaitu ruas garis PA ≅ ruas garis PB ?

Rencana      : Gambar/Sketsa permasalahan :

                                 Harus dibuktikan ∆PEA ≅ ∆PEB agar diperoleh PA ≅ PB

Bukti tahap 1

Pernyataan	Alasan
1.       adalah ruas garis membagi dua dan tegak lurus (^) AB 2.      Ukuran sudut PEA dan sudut PEB sama yaitu ∠PEA ≅ ∠PEB 3.      Ukuran panjang ruas garis AE ≅ EB 4.   Ruas garis PE ≅ Ruas garis PE 5.     ∆PEA ≅ ∆PEB 6.     PA ≅ PB	1.      Diketahui 2.      Kedua sudut adalah sudut siku-siku. Semua sudut siku-siku kongruen 3.      Agar dapat membagi dua sama besar maka ruas garis dibagi menjadi bagian-bagian yang kongruen 4.      Sifat refleksif 5.      Kekongruenan dua segitiga (s.a.s) 6.      Hukum kongruensi ≅

 Tahap 2       :  Akan dibuktikan untuk sembarang titik memenuhi kondisi berikut :

Diketahui    : Sembarang titik Q yang berjarak sama dari titik A dan B yaitu ruas garis QA ≅ ruas garis QB

Ditanyakan    : Apakah Q berada pada sebuah ruas garis yang membagi dua dan tegak lurus AB

Rencana      : Gambar/Sketsa Masalah bahwa QG ⊥ AB

                       Akan dibuktikan dengan menggunakan segitiga-segitiga kongruen bahwa QG membagi dua AB

Bukti Tahap 2

Jadi teorema 2.3 terbukti

untuk lebih mengerti bagaimana menyelesaikan masalah dengan polya. Mari lihat contoh berikut :

Terdapat dua buah pelampung pada sebuah danau. Seorang perenang berenang di danau tersebut sedemikian sehingga ia selalu berjarak tetap (konstan) terhadap kedua pelampung tersebut. Deskripsikan jalur renang yang ditempuh oleh perenang tersebut.

Tahap pemecahan masalah :

1)         Understanding the Problem

a.         Nyatakan masalah dengan kalimatmu sendiri !

Misalkan kedua pelampung adalah titik A dan B dan perenang adalah titik C

Misalkan jarak C ke A adalah d_AC dan jarak C ke B adalah d_CB.

Maka posisi perenang yaitu C terhadap A dan B adalah kumpulan titik-titik sehingga d_CA dan d_CB selalu tetap. Berbentuk apakah kumpulan  titik-titik tersebut ?

b.        Tentukan apa saja yang akan ditemukan/dicari/diselesaikan !

Bentuk kumpulan titik-titik sehingga d_CA dan d_CB selalu tetap.

c.         Apa saja yang tidak diketahui dari permasalahan itu ?

Jarak titik A ke B

d.        Informasi apa saja yang kamu peroleh dari permasalahan itu ?

Titik A dan B berbeda posisi

Jarak d_CA dan d_CB selalu tetap yaitu d_CA = d_CB untuk meskipun posisi C berubah-ubah

2)        Devising a Plan

Strategi pemecahan masalah yang mungkin dapat digunakan untuk menyelesaikan masalah :

a.          Membuat diagram / gambar

Menggambarkan posisi titik A, B, dan C sesuai kondisi masalah.

b.        Menguji masalah yang relevan dan memeriksanya apa dapat digunakan

Memeriksa jika ada satu atau lebih teorema dasar kedudukan titik yang menyerupai masalah ini.

3)        Carrying Out the Plan

a.       Membuat diagram / gambar

b.        Memeriksa jika ada teorema kedudukan titik yang sesuai

Teorema 2.3 : Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garis  dan membagi  menjadi dua bagian sama besar

Berdasarkan gambar dan teorema tersebut maka kedudukan perenang terhadap kedua pelampung tersebut dapat dideskripsikan sebagai sebuah ruas garis yang tegak lurus terhadap ruas garis yang menghubungkan kedua pelampung yaitu  dan membagi ruas garis  menjadi dua bagian sama panjang seperti digambarkan sebagai berikut.

4)        Looking Back

Langkah terakhir pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya dengan cara :

a.         Memeriksa dengan pembuktian : buktikan teorema 2.3 berdasarkan masalah tersebut secara deduktif

b.        Menginterpretasikan penyelesaian permasalahan ini berdasarkan argumentasi (reasonable) dengan menggunakan koordinat dan aljabar

Misalkan koordinat titik C(x, y) di mana d_CA = d_CB dengan koordinat A(x_a, y_a) dan B(x_b, y_b) maka dapat dibuktikan untuk posisi C di C₁(x₁, y₁), C₂(x₂, y₂), … Cn(x_n, y_n) yaitu : (a) jika ruas garis  tegak lurus sumbu x maka y₁ = y₂ = … = y_n

(b) jika ruas garis  tegak lurus sumbu y maka x₁ = x₂ = … = x_n

Selanjutnya harus dibuktikan bahwa garis C₁C₂ tegak lurus

Dengan bantuan geogebra dapat dilakukan simulasi untuk menunjukkan solusi  untuk tiga posisi C yang berbeda-beda sebagai berikut.

Semoga bermanfaat yaaaa :*